
When the electron is in this lowest energy orbit, the atom is said to be in its ground electronic state (or simply ground state). Thus, the electron in a hydrogen atom usually moves in the n = 1 orbit, the orbit in which it has the lowest (most negative) energy. One of the fundamental laws of physics is that matter is most stable with the lowest possible energy. The lowest few energy levels of hydrogen are shown in Figure 3. The more negative the calculated value, the lower the energy. Quantum numbers and energy levels in a hydrogen atom.
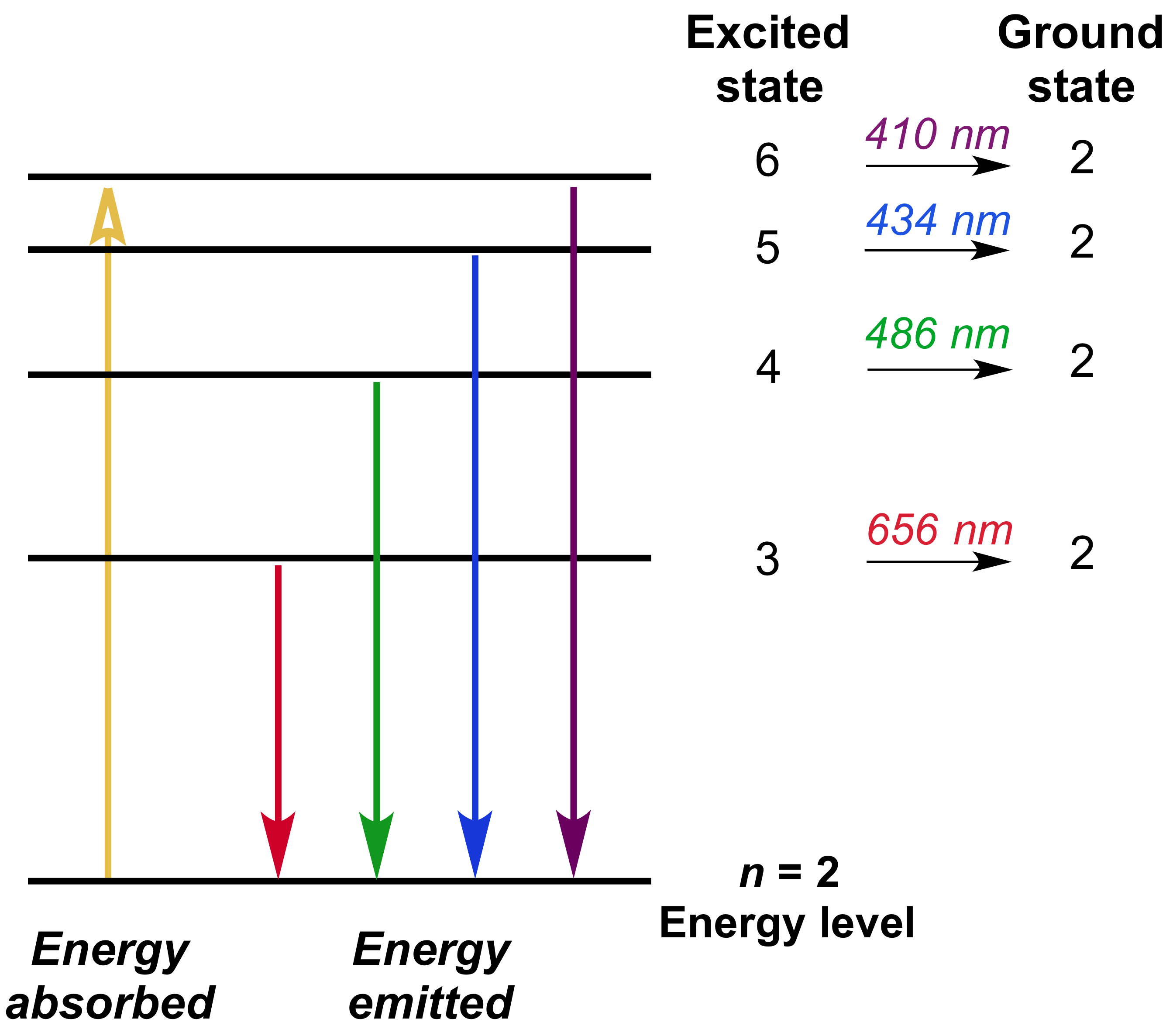
Since the Rydberg constant was one of the most precisely measured constants at that time, this level of agreement was astonishing and meant that Bohr’s model was taken seriously, despite the many assumptions that Bohr needed to derive it. When Bohr calculated his theoretical value for the Rydberg constant, R ∞, and compared it with the experimentally accepted value, he got excellent agreement, where A = 2.179 × 10 –18 J. In this expression, A is a constant comprising fundamental constants such as the electron mass and charge and Planck’s constant, Z is the atomic number for H which is 1, and n is the energy level. That equation is the following one, in which k is a constant: Even more puzzling, in 1885, Johann Balmer was able to derive an empirical equation that related the four visible wavelengths of light emitted by hydrogen atoms to whole integers. The origin of discrete spectra in atoms and molecules was extremely puzzling to scientists in the late nineteenth century, since according to classical electromagnetic theory, only continuous spectra should be observed. This sign shows the elaborate artistic effects that can be achieved. Neon signs operate by exciting a gas at low partial pressure using an electrical current. Each element displays its own characteristic set of lines, as do molecules, although their spectra are generally much more complicated. Fluorescent light bulbs and neon signs operate in this way ( Figure 2). (10 Å = 1 nm)Įxciting a gas at low partial pressure using an electrical current, or heating it, will produce line spectra. Compare the two types of emission spectra: continuous spectrum of white light (top) and the line spectra of the light from excited sodium, hydrogen, calcium, and mercury atoms. Passing the light through a prism produces a line spectrum, indicating that this light is composed of photons of four visible wavelengths, as shown in Figure 1. For example, when an electric discharge passes through a tube containing hydrogen gas at low pressure, the H 2 molecules are broken apart into separate H atoms and we see a blue-pink color. Each emission line consists of a single wavelength of light, which implies that the light emitted by a gas consists of a set of discrete energies. In contrast to continuous spectra, light can also occur as discrete or line spectra having very narrow line widths interspersed throughout the spectral regions such as those shown in Figure 1, bottom. These continuous spectra can often be approximated by blackbody radiation curves at some appropriate temperature. Incandescent (glowing) solids such as tungsten filaments in incandescent lights also give off light that contains all wavelengths of visible light. As can be seen in the continuous spectrum ( Figure 1, top), sunlight also contains UV light (shorter wavelengths) and IR light (longer wavelengths) that can be detected using instruments but that are invisible to the human eye. You can see all the visible wavelengths of light present in sunlight by using a prism to separate them. Most of the light generated from stars (including our sun) is produced in this fashion.
ATOMIC EMISSION SPECTRUM VS ENERGY LEVELS SERIES
Photons produced in this manner have a range of energies, and thereby produce a continuous spectrum in which an unbroken series of wavelengths is present. As seen in the previous section, when solids, liquids, or condensed gases are heated sufficiently, they radiate some of the excess energy as light. | Key Concepts and Summary | Key Equations | Glossary | End of Section Exercises | Emission Line SpectraĪnother paradox within the classical electromagnetic theory that scientists in the late nineteenth century struggled with concerned the light emitted from atoms and molecules.
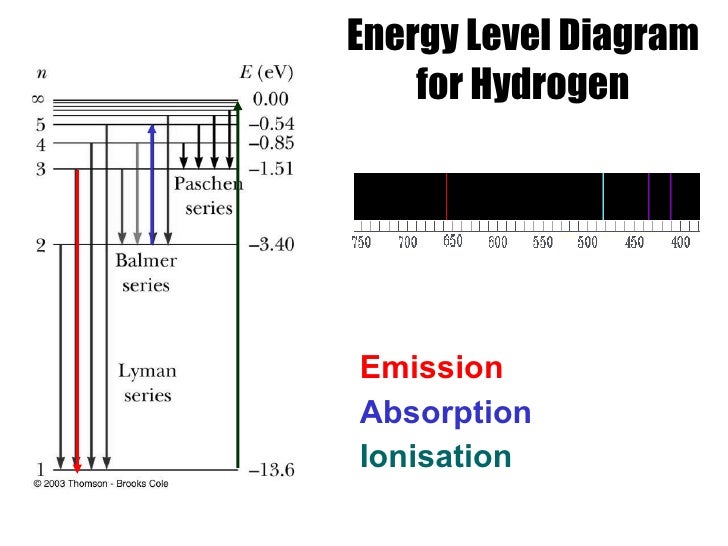
Predict the observed emission and absorption frequencies and wavelengths of photons using the Bohr theory.Summarize the connection between discrete line spectra and how energy levels of atoms are quantized.


 0 kommentar(er)
0 kommentar(er)
